https://doi.org/10.1140/epjp/s13360-021-01298-y
Regular Article
Logarithmic-corrected Einstein–Gauss–Bonnet inflation compatible with GW170817
Department of Physics, Aristotle University of Thessaloniki, 54124, Thessaloniki, Greece
Received:
24
January
2021
Accepted:
4
March
2021
Published online:
11
March
2021
In this paper, we investigate the inflationary phenomenology of an Einstein–Gauss–Bonnet theory with the extension of a logarithmic modified f(R) gravity, compatible with the GW170817 event. The main idea of our work is to study different results for an almost linear Ricci scalar through logarithmic corrections and examine whether such model is viable. First of all, the theoretical framework under slow-roll evolution of the scalar field is presented and also the formalism of the constant-roll evolution making predictions for the non-Gaussianities of the models is developed, since the constant-roll evolution is known to enhance non-Gaussianities. As shown, the non-Gaussianities are of the order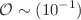 
. Furthermore, the slow-roll indices and the observational indices of inflation are calculated for several models of interest. As demonstrated, the phenomenological viability of the models at hand is achieved for a wide range of the free parameters and the logarithmic term has a minor contribution to numerical calculations, as expected.
© The Author(s) 2021
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
