Eur. Phys. J. Plus (2021) 136: 282
https://doi.org/10.1140/epjp/s13360-021-01261-x

Regular Article

q-Cat states revisited: two families in a Fock representation space of q-oscillator algebra with different nonclassical behaviors

Department of Theoretical Physics and Astrophysics, Faculty of Physics, University of Tabriz, P. O. Box 51666-16471, Tabriz, Iran

^a hfakhri@tabrizu.ac.ir

Received: 1 September 2020
Accepted: 21 February 2021
Published online: 3 March 2021

Abstract

This paper has been motivated by our previous paper (Eur. Phys J Plus 135:253, 2020) on q-coherent states of the Arik–Coon q-oscillator. The quadratic powers of unbounded and bounded annihilation operators associated with the Arik–Coon q-oscillator are used to obtain two different families of the even and odd q-cat states for in even and odd subspaces of the Fock representation space of the system. The resolutions of the identity condition for q-cat states of the unbounded and bounded annihilation operators are realized by two appropriate positive definite q-measures in the q-integral on the whole complex plane and a disk in radius 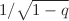, respectively. It is shown that the antibunching effect and sub-Poissonian statistics as well as the bunching effect and super-Poissonian statistics are simultaneously exhibited by the first and second families of q-cat states, respectively. Otherwise, a fixed observation cannot be concluded. The strong and weak squeezing conditions for two different types of q-generalizations of the position and momentum quadratures, corresponding to the unbounded and bounded annihilation operators, on their associated even and odd q-cat states are considered. Using an example, we show that contrary to the odd q-cat states of the first family that exhibit both strong and weak squeezing effects by both quadratures, the ones of the second family demonstrate only the weak squeezing.