https://doi.org/10.1140/epjp/s13360-020-00714-z
Regular Article
Inverse scattering transform for the complex short-pulse equation by a Riemann–Hilbert approach
1
Department of Mathematics, University at Buffalo, 14260, Buffalo, NY, USA
2
Department of Applied Mathematics and Statistics, Montclair State University, 07043, Montclair, NJ, USA
3
School of Mathematical and Statistical Sciences, The University of Texas Rio Grande Valley, 78539, Edinburg, TX, USA
Received:
31
May
2020
Accepted:
26
August
2020
Published online:
12
September
2020
In this paper, we develop the inverse scattering transform (IST) for the complex short-pulse equation (CSP) on the line with zero boundary conditions at space infinity. The work extends to the complex case the Riemann–Hilbert approach to the IST for the real short-pulse equation proposed by A. Boutet de Monvel, D. Shepelsky and L. Zielinski in 2017. As a byproduct of the IST, soliton solutions are also obtained. Unlike the real SPE, in the complex case discrete eigenvalues are not necessarily restricted to the imaginary axis, and, as consequence, smooth 1-soliton solutions exist for any choice of discrete eigenvalue  with
with  . The 2-soliton solution is obtained for arbitrary eigenvalues
. The 2-soliton solution is obtained for arbitrary eigenvalues 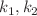 , providing also the breather solution of the real SPE in the special case
, providing also the breather solution of the real SPE in the special case 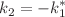 .
.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2020




