From generalized Fourier transforms to spectral curves for the Manakov hierarchy. I. Generalized Fourier transforms

V. S. Gerdjikov; A. O. Smirnov; V. B.  Matveev

doi:10.1140/epjp/s13360-020-00668-2

EPJ

From generalized Fourier transforms to spectral curves for the Manakov hierarchy. I. Generalized Fourier transforms

V. S. Gerdjikov¹^,2^a, A. O. Smirnov² and V. B. Matveev³^,4

¹ Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Sofia, Bulgaria
² Sankt-Petersburg State University of Aerospace Instrumentation, Sankt-Petersburg, Russia
³ Sankt-Petersburg Department of Steklov Mathematical Institute of Russian Academy of Sciences, Sankt-Petersburg, Russia
⁴ Institut de Mathématiques de Bourgogne - UMR 5584 CNRS, Université de Bourgogne - Franche Comté, Dijon, France

Received: 3 June 2020
Accepted: 3 August 2020
Published online: 17 August 2020

Abstract

The generalized Fourier transforms (GFTs) for the hierarchies of multi-component models of Manakov type are revisited. Our aim is to adapt GFT so that one could treat the whole hierarchy of nonlinear evolution equations simultaneously. To this end we consider the potential Q of the Lax operator L as local coordinate on some symmetric space depending on an infinite number of variables t, and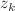

z_{k}

k = 1, 2, \dots

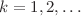$k=1, 2, \ldots$ . The dependence on

z_{k}

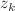is determined by the k-th higher flow (conserved density) of the hierarchy. Thus we have an infinite set of commuting operators with common fundamental analytic solution. We analyze the properties of the resolvent and thus determine the spectral properties of L. Then we derive the generalized Fourier transforms that linearize this hierarchy of NLEE and establish their fundamental properties as well as dynamical compatibility of each two pairs of such flows. Using the classical R-matrix approach we derive the Poisson brackets between all conserved quantities first assuming that Q is a quasi-periodic function of t. Next taking the limit when the period tends to

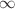\infty

$\infty$ , we derive the Poisson brackets between the scattering data of L. In addition we analyze a possible relation of our approach to the one based on the

τ

$\tau$ -function that could lead to multi-dimensional integrable equations.

In memory of Boris Dubrovin and Viktor Enol’skii.

Student Conference in Optics and Photonics 2024
October 2-4, 2024
Barcelona, Spain

EPJ

From generalized Fourier transforms to spectral curves for the Manakov hierarchy. I. Generalized Fourier transforms

Conference announcements