Eur. Phys. J. Plus (2020) 135: 641
https://doi.org/10.1140/epjp/s13360-020-00631-1

Regular Article

Noether-type Hamiltonian symmetry classification, first integrals and exact solutions of two classes of the generalized Ermakov’s systems

Centre For Mathematics and Statistical Sciences, Lahore School of Economics, 53200, Lahore, Pakistan

^a drrehana@lahoreschool.edu.pk

Received: 22 August 2019
Accepted: 24 July 2020
Published online: 10 August 2020

Abstract

In this paper, Noether-type Hamiltonian symmetry classification, first integrals and exact solutions of two classes of the generalized Ermakov’s systems, in plane polar form, are investigated by utilizing the Noether’s theorem in phase space (see Dorodnitsyn and Kozlov in J Eng Math 66:253–270, 2010). First, Noether-type Hamiltonian symmetry classification is performed for the generalized two-dimensional Ermakov’s system studied by Ray and Reid (Phys Lett A 71(4):317–318, 1979). 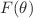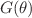The generalized Ermakov’s system involves two functions $F(\theta )$ and $G(\theta )$ satisfying 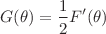$G(\theta )=\frac{1}{2}{F}^{\prime }(\theta )$. 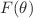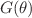For the arbitrary forms of functions $F(\theta )$ and $G(\theta )$, four first integrals are constructed. The angular momentum-type first integral known as Ermakov invariant is a consequence of the Hamiltonian symmetry having dependence on a momentum coordinate. And it corresponds to a generalized symmetry when analysis is performed in the Lagrangian perspective. Three first integrals are functionally independent, and thus generalized Ermakov’s systems are completely integrable. 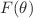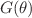The Noether’s theorem in phase space yields four different functional forms of $F(\theta )$ and $G(\theta )$ for which the generalized Ermakov’s system has the additional first integrals. These functional forms are new and not provided before in the literature. 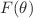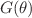Finally, the derived first integrals are utilized to construct the exact solutions for arbitrary $F(\theta )$ and $G(\theta )$ as well as for four different forms of these functions. A similar analysis is carried out for another form of the generalized Ermakov’s system studied by Athorne (Phys Lett A 151(8):407–411, 1990), and results are compared with the earlier works done in the literature.