https://doi.org/10.1140/epjp/s13360-020-00617-z
Regular Article
Soliton interactions in certain square matrix nonlinear Schrödinger systems
Department of Mathematics, University at Buffalo, 14260, Buffalo, NY, USA
Received:
28
May
2020
Accepted:
16
July
2020
Published online:
28
July
2020
This work deals with a class of square matrix nonlinear Schrödinger (MNLS) systems whose reductions include two equations that model hyperfine spin 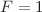 spinor Bose–Einstein condensates in the focusing and defocusing dispersion regimes, and two novel (mixed sign) equations that were recently shown to be integrable. Our main goal is to discuss the bright soliton solutions and their interactions for the focusing MNLS and for the two mixed sign systems within the framework of the inverse scattering transform. The nature of the solitons and their interactions depend on whether the associated norming constants (polarization matrices) are rank-one matrices (giving rise to ferromagnetic solitons) or full rank (corresponding to polar solitons). By computing the long-time asymptotics of the 2-soliton solutions, we determine how the polarization matrix of each soliton changes because of the interaction. Explicit formulas for the soliton interactions are given for all possible types of interacting solitons, namely ferromagnetic–ferromagnetic, polar–polar, and polar–ferromagnetic soliton interactions, and for all three inequivalent reductions of the MNLS systems that admit regular bright soliton solutions. We also present bound states, representing 2 solitons travelling with the same velocity, for all three systems.
spinor Bose–Einstein condensates in the focusing and defocusing dispersion regimes, and two novel (mixed sign) equations that were recently shown to be integrable. Our main goal is to discuss the bright soliton solutions and their interactions for the focusing MNLS and for the two mixed sign systems within the framework of the inverse scattering transform. The nature of the solitons and their interactions depend on whether the associated norming constants (polarization matrices) are rank-one matrices (giving rise to ferromagnetic solitons) or full rank (corresponding to polar solitons). By computing the long-time asymptotics of the 2-soliton solutions, we determine how the polarization matrix of each soliton changes because of the interaction. Explicit formulas for the soliton interactions are given for all possible types of interacting solitons, namely ferromagnetic–ferromagnetic, polar–polar, and polar–ferromagnetic soliton interactions, and for all three inequivalent reductions of the MNLS systems that admit regular bright soliton solutions. We also present bound states, representing 2 solitons travelling with the same velocity, for all three systems.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2020




