https://doi.org/10.1140/epjp/s13360-020-00388-7
Regular Article
An approximation to the Woods–Saxon potential based on a contact interaction
1
Departamento de Física Teórica, Atómica y Óptica and IMUVA, Universidad de Valladolid, 47011, Valladolid, Spain
2
Instituto de Física Rosario (CONICET-UNR), Bv. 27 de Febrero 210 bis, S2000EZP, Rosario, Argentina
3
Facultad de Ciencias Exactas, Ingeniería y Agrimensura (UNR), Av. Pellegrini 250, S2000BTP, Rosario, Argentina
4
Instituto de Estudios Nucleares y Radiaciones Ionizantes (UNR), Riobamba y Berutti, S2000EKA, Rosario, Argentina
* e-mail: manuelgadella1@gmail.com
Received:
9
March
2020
Accepted:
7
April
2020
Published online:
27
April
2020
We study a non-relativistic particle subject to a three-dimensional spherical potential consisting of a finite well and a radial 
contact interaction at the well edge. This contact potential is defined by appropriate matching conditions for the radial functions, thereby fixing a self-adjoint extension of the non-singular Hamiltonian. Since this model admits exact solutions for the wave function, we are able to characterize and calculate the number of bound states. We also extend some well-known properties of certain spherically symmetric potentials and describe the resonances, defined as unstable quantum states. Based on the Woods–Saxon potential, this configuration is implemented as a first approximation for a mean-field nuclear model. The results derived are tested with experimental and numerical data in the double magic nuclei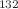 
Sn and 
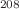Pb with an extra neutron.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2020
