Eur. Phys. J. Plus (2020) 135: 367
https://doi.org/10.1140/epjp/s13360-020-00370-3

Regular Article

Late time evolution of negatively curved FLRW models

¹ Mathematics Division, School of Science and Technology, University of Camerino, Camerino, Italy
² INFN, Sezione di Perugia, 06123, Perugia, Italy
³ Department of Marine Sciences, University of the Aegean, Lesbos, Greece
⁴ Present address: PhD School, University of Macerata, Macerata, Italy

^* e-mail: roberto.giambo@unicam.it

Received: 20 January 2020
Accepted: 30 March 2020
Published online: 21 April 2020

Abstract

We study the late time evolution of negatively curved Friedmann–Lemaître–Robertson–Walker (FLRW) models with a perfect fluid matter source and a scalar field nonminimally coupled to matter. Since under mild assumptions on the potential V, it is already known—see e.g., Giambò and Miritzis (Class Quantum Grav 27:095003, 2010)—that equilibria corresponding to nonnegative local minima for V are asymptotically stable, we classify all cases where one of the energy components eventually dominates. In particular for nondegenerate minima with zero critical value, we rigorously prove that if 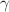, the parameter of the equation of state is larger than 2/3, then there is a transfer of energy from the fluid and the scalar field to the energy density of the scalar curvature. Thus, the scalar curvature, if present, has a dominant effect on the late evolution of the universe and eventually dominates over both the perfect fluid and the scalar field. The analysis in complemented with the case where V is exponential, and therefore the scalar field diverges to infinity.