Eur. Phys. J. Plus (2020) 135: 196
https://doi.org/10.1140/epjp/s13360-020-00234-w

Regular Article

Pentad and triangular structures behind the Racah matrices

¹ Moscow Institute for Physics and Technology, Dolgoprudny, Russia
² ITEP, Moscow, Russia
³ Institute for Information Transmission Problems, Moscow, Russia

^* e-mail: morozov.itep@mail.ru

Received: 26 June 2019
Accepted: 17 January 2020
Published online: 3 February 2020

Abstract

Somewhat unexpectedly, the study of the family of twisted knots revealed a hidden structure behind exclusive Racah matrices , which control non-associativity of the representation product in a peculiar channel . These are simultaneously symmetric and orthogonal and therefore admit two decompositions: as quadratic forms, , and as operators: . Here, and T consist of the eigenvalues of the quantum -matrices in channels and , respectively, S is the second exclusive Racah matrix for 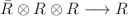(still orthogonal, but no longer symmetric) and is a triangular matrix. It can be further used to construct the KNTZ evolution matrix , which is also triangular and explicitly expressible through the skew Schur and Macdonald functions—what makes Racah matrices calculable. Moreover, is somewhat similar to Ruijsenaars Hamiltonian, which is used to define Macdonald functions, and gets triangular in the Schur basis. Discovery of this pentad structure 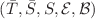, associated with the universal -matrix, can lead to further insights about representation theory, knot invariants and Macdonald–Kerov functions.