https://doi.org/10.1140/epjp/s13360-020-00233-x
Regular Article
Deformation characteristics of three-wave solutions and lump N-solitons to the (2 + 1)-dimensional generalized KdV equation
College of Mathematics and Statistics, Jishou University, Jishou, 416000, People’s Republic of China
* e-mail: tanwei1008@126.com
Received:
10
September
2019
Accepted:
8
January
2020
Published online:
10
February
2020
In this paper, the three-wave solution of (
)-dimensional generalized Korteweg-de Vries equation is obtained by using Hirotäs bilinear method and three-wave method. We study the deformation characteristics of three-wave solution by taking different parameter values. A new lump solution is obtained when we study the degenerate behavior of three-wave solutions. Besides, we give an existence theorem of the interaction between lump solution and different forms of N-solitons (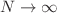
) and give a detailed calculation and proof process. Some new interaction solutions, such as lump N-solitons type, lump N-logarithmic type, lump cos–sin–exponential type, higher-order lump-type solutions, are used as examples to illustrate the correctness and effectiveness of the description theorem. We also give the evolutionary structure plots of the superposition behavior between lump solutions and solitons, and study the interaction behavior between lump-type solutions and solitons.
© Società Italiana di Fisica (SIF) and Springer-Verlag GmbH Germany, part of Springer Nature, 2020
