Eur. Phys. J. Plus (2020) 135: 155
https://doi.org/10.1140/epjp/s13360-019-00091-2

Regular Article

Anisotropic Lifshitz holography in Einstein–Proca theory with stable negative mass spectrum

¹ Instituto de Física, Benémerita Universidad Autónoma de Puebla, Apdo. Postal J-48, Puebla, 72570, Puebla, Mexico
² Facultad de Ciencias Físico Matemáticas, Benémerita Universidad Autónoma de Puebla, Apdo. Postal 165, 72000, Puebla, Mexico
³ Departamento de Matemáticas Aplicadas y Sistemas, Universidad Autónoma Metropolitana-Cuajimalpa, 05300, Mexico, CDMX, Mexico

^* e-mail: vmatlal@ifuap.buap.mx

Received: 20 November 2019
Accepted: 28 December 2019
Published online: 28 January 2020

Abstract

In this article, we focus on constructing a new family of spatially anisotropic Lifshitz spacetimes with arbitrary dynamical exponent z and constant negative curvature in 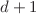dimensions within the framework of the Einstein–Proca theory with a single vector field. So far, this kind of anisotropic spaces has been constructed with the aid of a set of vector fields. We also consider the spatially isotropic case as a particular limit. The constructed metric tensor depends on the spacetime dimensionality, the critical exponent and the Lifshitz radius; while, the curvature scalar depends just on the number of dimensions. We also obtain a novel spectrum with negative squared mass; we compute the corresponding Breitenlohner–Freedman bound and observe that the found family of spatially anisotropic Lifshitz spaces respects this bound. Hence, these new solutions are stable and can be useful within the gravity/condensed matter theory holographic duality, since the spectrum with negative squared mass is complementary to the positive ones already known in the literature. We also examine the null energy condition and show that it is essentially satisfied along all the boundary directions, i.e., along all directions, except the r one, of our Lifshitz spacetime with the corresponding consistency conditions imposed on the scaling exponents.