https://doi.org/10.1140/epjp/i2019-12967-4
Regular Article
Singular limit in a nonlinear quantum field
1
Université de la Côte d’Azur - Observatoire de la Côte d’Azur, 06304, Nice Cedex, France
2
Science Institute, University of Iceland, Dunhaga 3, IS-107, Reykjavik, Iceland
* e-mail: Gilbert.Reinisch@oca.eu
Received:
22
June
2019
Accepted:
27
August
2019
Published online:
15
November
2019
The self-consistent mean-fied Schrödinger-Poisson model of quantum-dot helium is described in the mixed-state approximation of a two-level nonlinear quantum system (G. Reinisch, M. Gazeau, Eur. Phys. J. Plus 131, 220 (2016)). We investigate the strong nonlinear limit of vanishing harmonic confinement. We find that the two corresponding trajectories in the appropriate phase-space bifurcate from the Thomas-Fermi fixed point to a final singular statistical equilibrium state that is defined by equal population of the two energy levels as a result of eigenstate overlap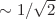 
between their respective nonlinear eigenstates. Further increase of nonlinearity, i.e. of eigenstate overlap, yields population inversion and therefore instability. At equilibrium, a black-body residual photon field is set up when considering the single-photon lowest-order QED description of the Coulomb interaction between the two electrons. We point out the possible interest of such an equilibrium state in the search of the Cooper-pair “pairing glue” of bound electron pairs in the degenerate Fermi gas of high-temperature superconductors, as well as its link with a recently renewed debate about the physical existence of QED mediating virtual photons (G. Jaeger, Entropy 21, 141 (2019)).
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2019
