https://doi.org/10.1140/epjp/i2019-12765-0
Regular Article
Modeling and simulation results of a fractional dengue model
1
Department of Mathematics, City University of Science and Information Technology, 25000, Peshawar, KP, Pakistan
2
College of Sciences and Humanities Studies Al-Kharj, Mathematics Department, Prince Sattam Bin Abdulaziz University, Al-Kharj, Saudi Arabia
3
Department of Engineering Mathematics and Physics, Faculty of Engineering, Mansoura University, 35516, Mansoura, Egypt
4
Department of Basic Science, Faculty of Computers and Informatics, Suez Canal University, 41522, Ismailia, Egypt
* e-mail: altafdir@gmail.com
Received:
16
April
2019
Accepted:
16
May
2019
Published online:
7
August
2019
Dengue fever is a vector-borne disease and is still epidemic in most countries of the world by providing so many outbreaks. The present paper investigates the dengue dynamics for the real cases reported in Pakistan in the period 2003–2015. The model is formulated and the associated properties are presented. We show, for the given period, a basic reproduction,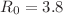 
. The parameters are parameterized for model simulation by using the leaset square curve fitting in MATLAB. We use the Caputo derivative and formulate the fractional dengue model. The stability analysis for the fractional dengue model in both disease-free and endemic cases is presented. We show that, in the disease-free case, the fractional dengue model is locally and globally stable when 
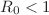. Then, we prove the model stability in the endemic case and present the results for 
. We provide some graphical illustrations and show that the dengue model with fractional derivative is more useful than that of the integer order model.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2019
