https://doi.org/10.1140/epjp/i2019-12585-2
Regular Article
A new approach for higher-order difference equations and eigenvalue problems via physical potentials
Firat University, Science Faculty, Department of Mathematics, 23119, Elazig, Turkey
* e-mail: ozarslanramazan@gmail.com
Received:
5
June
2018
Accepted:
19
February
2019
Published online:
6
June
2019
In the present paper the variation of parameters method for the N -th-order non-homogeneous linear ordinary difference equations with constant coefficient is introduced by means of the delta exponential function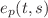 
. Thanks to this new advantageous approach, one can investigate the solution of higher-order difference equations which can be considered important for many mathematical models. Moreover, we bring forth the method with three difference eigenvalue problems involving the second-order Sturm-Liouville problem, called one-dimensional Schrödinger equation, with Coulomb potential, hydrogen atom equation and the fourth-order relaxation difference equation. Sum representations of the solutions of the second-order discrete Sturm-Liouville problem having Coulomb potential and hydrogen atom equation are found out. In addition, we get analytical solution of the fourth-order discrete relaxation problem by the variation of parameters method via delta exponential and delta trigonometric functions.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2019
