https://doi.org/10.1140/epjp/i2019-12520-7
Regular Article
General dynamic properties of conduction electron within the first Brillouin zone of graphene
Taras Shevchenko National University of Kyiv, 64/13 Volodymyrska Street, City of Kyiv, Ukraine
* e-mail: lshmel@univ.kiev.ua
Received:
3
May
2018
Accepted:
12
November
2018
Published online:
30
January
2019
Dispersion law of an electron (as a quasiparticle in the graphene conduction band) is sufficiently complex to construct its generalized analytic dynamics. This is due to such a “mixture” of the wave vector components that the dispersion law (which is also the quasiparticle Hamiltonian) cannot be “factored” into two summands containing only one component of the wave vector. It was established that within the first Brillouin zone of graphene there is a sufficiently large region, 
; 
, in which it is possible to construct an approximate dispersion law. Based on this, the corresponding energy range of electron injection was estimated for graphene: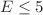 
eV. This range completely “covers” the entire range used in applications for graphenes, and the estimation itself became possible due to the generalized de Broglie relation between the components of the wave and mechanical momenta. In this case, the velocity and the effective mass of the injected electron were determined to determine the components of the mechanical momentum. A Lagrangian for an electron was also determined, as a quasiparticle, with respect to its wave description. Such a Lagrangian is a summand in the phase of electron wave function at its quantum description.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2019
