On the dimensional reduction of quadratic higher-derivative gravitational terms

M. D. Pollock

doi:10.1140/epjp/i2019-12376-9

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2019) 134: 22
https://doi.org/10.1140/epjp/i2019-12376-9

Regular Article

On the dimensional reduction of quadratic higher-derivative gravitational terms

M. D. Pollock^*

V. A. Steklov Mathematical Institute, Russian Academy of Sciences, Ulitsa Gubkina 8, 119991, Moscow, Russia

^* e-mail: mdp30@cam.ac.uk

Received: 24 June 2018
Accepted: 4 November 2018
Published online: 15 January 2019

Abstract

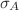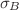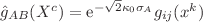
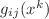Gravitational Lagrangian theories, that are formulated initially in $D (\equiv 4+N)$ dimensions, produce scalar moduli $\sigma_{A}$ , $\sigma_{B}$ upon reduction to four dimensions, via the metric decomposition $\hat{g}_{AB} (X^{c}) = {\rm e}^{-\sqrt{2} \kappa_{0} \sigma_{A}} g_{ij}(x^{k})$ $\otimes {\rm e}^{2 \kappa_{0} \sigma_{B}/\sqrt{N}} \bar{g}_{\mu\nu} (y^{\xi})$ , where $\kappa_{0}^{2}$ is the bare four-dimensional gravitational coupling, while $g_{ij}(x^k)$ and $\bar{g}_{\mu\nu} (y^{\xi})$ are the physical four- and internal-space N-metrics, respectively. 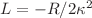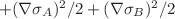After integration over the N-space, the four-Lagrangian resulting from the Einstein-Hilbert D-theory $\hat{L} = -{\rm e}^{-2\phi} [\hat{R}$ $+4(\hat{\nabla}\phi)^{2}]/2 \hat{\kappa}^{2}$ is $L=-R/2\kappa^{2}$ $+(\nabla \sigma_{A})^{2}/2 + (\nabla \sigma_{B})^{2}/2$ , in which the kinetic-energy terms for 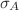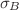$\sigma_{A}$ , $\sigma_{B}$ have canonical coefficients 1/2. These coefficients are modified, however, if 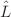$\hat{L}$ contains in addition quadratic higher-derivative terms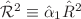 $\hat{\mathcal{R}}^{2} \equiv \hat{\alpha}_{1}\hat{R}^{2}$ $+ \hat{\alpha}_{2}\hat{R}_{AB} \hat{R}^{AB} + \hat{\alpha}_{3}\hat{R}_{ABCD}\hat{R}^{ABCD}$ , due to the rescaling under the conformal transformation $\hat{g}_{AB}\rightarrow {\rm e}^{-\sqrt{2}\kappa_{0} \sigma_{A}} g_{ij}$ , which is typically of the form $\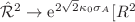hat{\mathcal{R}}^{2} \rightarrow {\rm e}^{2\sqrt{2} \kappa_{0} \sigma_{A}} [{R}^{2}$ $+\mathcal{R} (\nabla \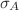sigma_{A,B})^2 + (\nabla \sigma_{A,B})^{4}]$ . 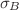Previously, we analyzed the effect of the terms $\mathcal{R}(\nabla \sigma_{A,B})^{2}$ quadratic in $\nabla \sigma_{A,B}$ , which in general lead to a mixing of $\sigma_{A}$ and $\sigma_{B}$ , and consequently instability at high energies. Here, we consider the quartic terms 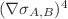$(\nabla \sigma_{A,B})^{4}$ , that also give rise to instabilities, both for arbitrary 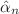$\hat{\alpha}_n$ and in the specific case of the heterotic superstring theory, for which 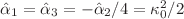$\hat{\alpha}_1= \hat{\alpha}_3 =-\hat{\alpha}_2/4=\kappa_{0}^{2}/{2}$ , and become significant if 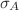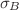$\sigma_{A}$ , $\sigma_{B}$ behave as massless scalars.