Eur. Phys. J. Plus (2018) 133: 382
https://doi.org/10.1140/epjp/i2018-12199-2

Regular Article

Theoretical and numerical investigations on solitary wave solutions of Gardner equation

¹ Armutlu Vocational School, Yalova University, Armutlu 77500, Yalova, Turkey
² Radiation Physics Laboratory, Department of Physics, Faculty of Sciences, Badji Mokhtar University, P.O. Box 12, 23000, Annaba, Algeria
³ Department of Mathematics, Central University of Haryana, 123029, Haryana, India
⁴ Department of Civil Engineering, Nigde Omer Halisdemir University, 51245, Nigde, Turkey

^* e-mail: akturgut@yahoo.com

Received: 30 May 2018
Accepted: 6 August 2018
Published online: 24 September 2018

Abstract

This paper formulates new hyperbolic functions ansatze to construct exact solitary wave solutions of the Gardner (combined KdV-mKdV) equation and a finite element approach for the numerical solutions. A novel class of exact solitary wave solutions is derived. The conditions on the physical parameters for the existence of the obtained structures are also presented. Accuracy of the proposed numerical scheme is assessed in terms of L₂ and 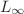error norms. Numerical experiments demonstrate the accuracy and robustness of the method which can be further used for solving other nonlinear problems.