Eur. Phys. J. Plus (2018) 133: 235
https://doi.org/10.1140/epjp/i2018-12067-1

Regular Article

Evolution and metric signature change of maximally symmetric spaces under the Ricci flow

Instituto de Física-LRT, Benemérita Universidad Autónoma de Puebla, 72570, Puebla, Puebla, Mexico

^* e-mail: rcartas@ifuap.buap.mx

Received: 23 February 2018
Accepted: 12 May 2018
Published online: 22 June 2018

Abstract

In this work we present solutions to the Ricci flow equations in arbitrary dimensions, in particular for the 3d and 4d cases. We start by considering the 3d case and note that our solutions belong to the family of maximally symmetric spaces that can be extended to the 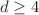case following an analogous treatment. These solutions can be divided into two scenarios: maximally symmetric spaces with positive curvature, i.e. de Sitter spaces, and maximally symmetric spaces with negative curvature, i.e. anti-de Sitter spaces. We show that between both scenarios there is a critical point where the curvature blows up along the flow. Also the solutions for 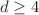satisfy the flow equations with Riemannian or pseudo-Riemannian metrics, due to the fact that the considered maximally symmetric spaces do not depend either on time or on the angular coordinates, yielding equations that depend only on the radial coordinate and the Ricci flow parameter. Additionally, we find an interesting effect of the flow consisting in a change of the signature of the metric when passing the singular point. Besides the signature change, the sign of the curvature also experiences a transition from positive to negative curvature, either with Riemannian or pseudo-Riemannian metrics throughout the singular point.