https://doi.org/10.1140/epjp/i2018-11851-1
Regular Article
Fractional analysis for nonlinear electrical transmission line and nonlinear Schroedinger equations with incomplete sub-equation
1
Pure Physics Laboratory, Group of Nonlinear Physics and Complex Systems, Department of Physics Faculty of Sciences, University of Douala, P.O. Box 24154, Douala, Cameroon
2
Nonlinear Physics and Complex Systems Group, Department of Physics, The Higher Teacher’s Training College, University of Yaounde I, P.O. Box 47, Yaounde, Cameroon
3
Abdus Salam ICTP, Strada Costiera 11, I-34151, Trieste, Italy
* e-mail: nguenang@yahoo.com
Received:
2
October
2017
Accepted:
29
December
2017
Published online:
2
February
2018
We use the fractional complex transform with the modified Riemann-Liouville derivative operator to establish the exact and generalized solutions of two fractional partial differential equations. We determine the solutions of fractional nonlinear electrical transmission lines (NETL) and the perturbed nonlinear Schroedinger (NLS) equation with the Kerr law nonlinearity term. The solutions are obtained for the parameters in the range (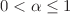
) of the derivative operator and we found the traditional solutions for the limiting case of 
. We show that according to the modified Riemann-Liouville derivative, the solutions found can describe physical systems with memory effect, transient effects in electrical systems and nonlinear transmission lines, and other systems such as optical fiber.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2018
