https://doi.org/10.1140/epjp/i2017-11752-9
Regular Article
Jacobi elliptic solutions, solitons and other solutions for the nonlinear Schrödinger equation with fourth-order dispersion and cubic-quintic nonlinearity
1
Department of Mathematics, Faculty of Sciences, Zagazig University, Zagazig, Egypt
2
Department of Mathematics, Faculty of Education and Science, Taiz University, Taiz, Yemen
* e-mail: alnowehy2010@yahoo.com
Received:
26
July
2017
Accepted:
12
October
2017
Published online:
13
November
2017
Based on several integration tools, namely the Riccati equation method, the Bernoulli equation method, the extended auxiliary equation method, the new mapping method and the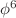 
-model expansion method, we obtain many exact solutions including the optical bright-dark-singular soliton solutions, Jacobi elliptic solutions and trigonometric function solutions of the nonlinear Schrödinger equation (NLSE) with fourth-order dispersion and cubic-quintic nonlinearity, self-steeping and self-frequency shift effects which describes the propagation of an optical pulse in optical fibers. We compare the results yielding from these integration tools together with each others. Also, a comparison between our results in this paper and the well-known results are given.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2017
