Eur. Phys. J. Plus (2017) 132: 436
https://doi.org/10.1140/epjp/i2017-11698-x

Regular Article

Stability analysis of an oscillating cylinder

Department of Mathematics, University of the Punjab, Quaid-e-Azam Campus, 54590, Lahore, Pakistan

^* e-mail: msharif.math@pu.edu.pk

Received: 12 May 2017
Accepted: 9 September 2017
Published online: 23 October 2017

Abstract

This paper is devoted to studying the dynamical instability of homogeneous as well as relativistic polytropic cylindrical spacetime under radial oscillations. We follow the Eulerian and Lagrangian approaches to find the perturbed dynamical equation. We use the conservation of baryon number to evaluate perturbed pressure as well as the adiabatic index. A variational method is developed to determine frequencies of oscillation which define stability conditions for the gaseous cylinder. It is found that dynamical instability occurs if the gaseous cylinder contracts to the radius 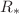. We conclude that the polytropic model of index 3 is more stable as compared to other cylindrical configurations.