Effect of vertical quasi-periodic vibrations on the stability of the free surface of a fluid layer

Mohamed Yagoubi; Saïd Aniss

doi:10.1140/epjp/i2017-11514-9

EPJ

a
b
c
d
e
ap
st
h
plus
ds
pv
ti
qt
am
n

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2017) 132: 226
https://doi.org/10.1140/epjp/i2017-11514-9

Regular Article

Effect of vertical quasi-periodic vibrations on the stability of the free surface of a fluid layer

Mohamed Yagoubi and Saïd Aniss^*

Laboratory of Mechanics, Faculty of Sciences Aïn Chock, University Hassan II, Casablanca, Morocco

^* e-mail: s.aniss@etude.univcasa.ma

Received: 3 December 2016
Accepted: 24 April 2017
Published online: 24 May 2017

Abstract

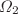In this paper we examine the effect of vertical quasi-periodic oscillations on the stability of the free surface of a horizontal liquid layer. The quasi-periodic motion considered here is characterized by two incommensurate frequencies, $\Omega_{1}$ and $\Omega_{2}$ , i.e. the ratio 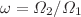$\omega=\Omega_{2}/\Omega_{1}$ is irrational. The linear quasi-periodic oscillator, corresponding to the governing equations of the Faraday instability, is treated using the harmonic balance method developed by Rand et al. and Zounes and Rand, and by numerical methods using the Floquet analysis and knowing that an irrational number can be approximated by a rational number. We determine the marginal stability curves in terms of reduced amplitude forcing and wave number for inviscid and viscous liquids. For both cases, we show that the neutral stability curves depend strongly on the frequency ratio of oscillations, 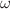$\omega$ , when this parameter is below 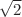$\sqrt{2}$ . Beyond this value, there is no effect of 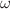$\omega$ and the first resonance occurs always at the wave number corresponding to the value of the natural frequency squared, $\delta=0.25$ . 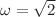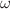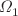Below the value $\omega=\sqrt{2}$ , variations of the wave number as a function of $\omega$ and $\Omega_{1}^{}$ are presented for the inviscid case. 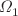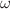However, for the viscous case, we show the existence of the bicritical points and we present the instability threshold versus $\Omega_{1}^{}$ for different values of $\omega$ .