https://doi.org/10.1140/epjp/i2016-16313-2
Regular Article
Second-order differential equations for bosons with spin 
and in the bases of general tensor-spinors of rank 2j
Instituto de Física, Universidad Autónoma de San Luis Potosı, Av. Manuel Nava 6, S.L.P. 78290, San Luis Potosı, Mexico
* e-mail: mariana@ifisica.uaslp.mx
Received:
22
May
2016
Accepted:
16
August
2016
Published online:
12
September
2016
A boson of spin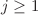 
can be described in one of the possibilities within the Bargmann-Wigner framework by means of one sole differential equation of order twice the spin, which however is known to be inconsistent as it allows for non-local, ghost and acausally propagating solutions, all problems which are difficult to tackle. The other possibility is provided by the Fierz-Pauli framework which is based on the more comfortable to deal with second-order Klein-Gordon equation, but it needs to be supplemented by an auxiliary condition. Although the latter formalism avoids some of the pathologies of the high-order equations, it still remains plagued by some inconsistencies such as the acausal propagation of the wave fronts of the (classical) solutions within an electromagnetic environment. We here suggest a method alternative to the above two that combines their advantages while avoiding the related difficulties. Namely, we suggest one sole strictly 
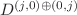representation specific second-order differential equation, which is derivable from a Lagrangian and whose solutions do not violate causality. The equation under discussion presents itself as the product of the Klein-Gordon operator with a momentum-independent projector on Lorentz irreducible representation spaces constructed from one of the Casimir invariants of the spin-Lorentz group. The basis used is that of general tensor-spinors of rank 2j .
© Società Italiana di Fisica and Springer-Verlag Berlin Heidelberg, 2016
