https://doi.org/10.1140/epjp/i2014-14178-y
Regular Article
On the transition from the quantum to the classical regime for massive scalar particles: A spatiotemporal approach
1
Sezione INFN di Firenze, Polo Scientifico, Via Sansone 1, 50019, Sesto Fiorentino (FI), Italy
2
Dipartimento di Fisica, Università di Parma, Parco Area Scienze 7/A, 43134, Parma, Italy
* e-mail: lusanna@fi.infn.it
Received:
12
May
2014
Revised:
16
July
2014
Accepted:
21
July
2014
Published online:
22
August
2014
If the classical structure of space-time is assumed to define an a priori scenario for the formulation of quantum theory (QT), the coordinate representation of the solutions
ψ(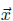 ,t) (ψ(
,t) (ψ(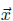 1,...,
1,...,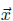 N,t))
of the Schroedinger equation of a quantum system containing one (N) massive scalar particle has a preferred status. Let us consider all of the solutions admitting a multipolar expansion of the probability density function
ρ(
N,t))
of the Schroedinger equation of a quantum system containing one (N) massive scalar particle has a preferred status. Let us consider all of the solutions admitting a multipolar expansion of the probability density function
ρ(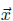 ,t) = |ψ(
,t) = |ψ(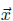 ,t)|2
(and more generally of the Wigner function) around a space-time trajectory
,t)|2
(and more generally of the Wigner function) around a space-time trajectory
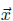 c(t)
to be properly selected. For every normalized solution
(∫d3xρ(
c(t)
to be properly selected. For every normalized solution
(∫d3xρ(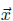 ,t) = 1)
there is a privileged trajectory implying the vanishing of the dipole moment of the multipolar expansion: it is given by the expectation value of the position operator
⟨ψ(t)|
,t) = 1)
there is a privileged trajectory implying the vanishing of the dipole moment of the multipolar expansion: it is given by the expectation value of the position operator
⟨ψ(t)| |ψ(t)⟩ =
|ψ(t)⟩ = 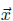 c(t).
Then, the special subset of solutions
ψ(
c(t).
Then, the special subset of solutions
ψ(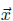 ,t)
which satisfy Ehrenfest’s Theorem (named thereby Ehrenfest monopole wave functions (EMWF)), have the important property that this privileged classical trajectory
,t)
which satisfy Ehrenfest’s Theorem (named thereby Ehrenfest monopole wave functions (EMWF)), have the important property that this privileged classical trajectory
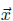 c(t)
is determined by a closed Newtonian equation of motion where the effective force is the Newtonian force plus non-Newtonian terms (of order ħ2 or higher) depending on the higher multipoles of the probability distribution ρ. Note that the superposition of two EMWFs is not an EMWF, a result to be strongly hoped for, given the possible unwanted implications concerning classical spatial perception. These results can be extended to N-particle systems in such a way that, when N classical trajectories with all the dipole moments vanishing and satisfying Ehrenfest theorem are associated with the normalized wave functions of the N-body system, we get a natural transition from the 3N-dimensional configuration space to the space-time. Moreover, these results can be extended to relativistic quantum mechanics. Consequently, in suitable states of N quantum particle which are EMWF, we get the “emergence” of corresponding “classical particles” following Newton-like trajectories in space-time. Note that all this holds true in the standard framework of quantum mechanics, i.e. assuming, in particular, the validity of Born’s rule and the individual system interpretation of the wave function (no ensemble interpretation). These results are valid without any approximation (like ħ → 0, big quantum numbers, etc.). Moreover, we do not commit ourselves to any specific ontological interpretation of quantum theory (such as, e.g., the Bohmian one). We will argue that, in substantial agreement with Bohr’s viewpoint, the macroscopic description of the preparation, certain intermediate steps and the detection of the final outcome of experiments involving massive particles are dominated by these classical “effective” trajectories. This approach can be applied to the point of view of de-coherence in the case of a diagonal reduced density matrix ρred (an improper mixture) depending on the position variables of a massive particle and of a pointer. When both the particle and the pointer wave functions appearing in ρred are EMWF, the expectation value of the particle and pointer position variables becomes a statistical average on a classical ensemble. In these cases an improper quantum mixture becomes a classical statistical one, thus providing a particular answer to an open problem of de-coherence about the emergence of classicality.
c(t)
is determined by a closed Newtonian equation of motion where the effective force is the Newtonian force plus non-Newtonian terms (of order ħ2 or higher) depending on the higher multipoles of the probability distribution ρ. Note that the superposition of two EMWFs is not an EMWF, a result to be strongly hoped for, given the possible unwanted implications concerning classical spatial perception. These results can be extended to N-particle systems in such a way that, when N classical trajectories with all the dipole moments vanishing and satisfying Ehrenfest theorem are associated with the normalized wave functions of the N-body system, we get a natural transition from the 3N-dimensional configuration space to the space-time. Moreover, these results can be extended to relativistic quantum mechanics. Consequently, in suitable states of N quantum particle which are EMWF, we get the “emergence” of corresponding “classical particles” following Newton-like trajectories in space-time. Note that all this holds true in the standard framework of quantum mechanics, i.e. assuming, in particular, the validity of Born’s rule and the individual system interpretation of the wave function (no ensemble interpretation). These results are valid without any approximation (like ħ → 0, big quantum numbers, etc.). Moreover, we do not commit ourselves to any specific ontological interpretation of quantum theory (such as, e.g., the Bohmian one). We will argue that, in substantial agreement with Bohr’s viewpoint, the macroscopic description of the preparation, certain intermediate steps and the detection of the final outcome of experiments involving massive particles are dominated by these classical “effective” trajectories. This approach can be applied to the point of view of de-coherence in the case of a diagonal reduced density matrix ρred (an improper mixture) depending on the position variables of a massive particle and of a pointer. When both the particle and the pointer wave functions appearing in ρred are EMWF, the expectation value of the particle and pointer position variables becomes a statistical average on a classical ensemble. In these cases an improper quantum mixture becomes a classical statistical one, thus providing a particular answer to an open problem of de-coherence about the emergence of classicality.
© Società Italiana di Fisica and Springer-Verlag Berlin Heidelberg, 2014




