Eur. Phys. J. Plus (2013) 128: 106
https://doi.org/10.1140/epjp/i2013-13106-1

Regular Article

Initial value problem for the linearized mean field Kramers equation with long-range interactions

Laboratoire de Physique Théorique (IRSAMC), CNRS and UPS, Université de Toulouse, F-31062, Toulouse, France

Received: 19 June 2013
Accepted: 15 July 2013
Published online: 12 September 2013

Abstract

We solve the initial value problem for the linearized mean field Kramers equation describing Brownian particles with long-range interactions in the 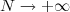limit. We show that the dielectric function can be expressed in terms of incomplete Gamma functions. The dielectric functions associated with the linearized Vlasov equation and with the linearized mean field Smoluchowski equation are recovered as special cases corresponding to the no friction limit and to the strong friction limit, respectively. Although the stability of the Maxwell-Boltzmann distribution is independent of the friction parameter, the evolution of the perturbation depends on it in a non-trivial manner. For illustration, we apply our results to self-gravitating systems, plasmas, and to the attractive and repulsive BMF models.