https://doi.org/10.1140/epjp/i2011-11062-4
Regular Article
Eigenvalue problem in two dimensions for an irregular boundary: Neumann condition
1
Centre for Theoretical Studies, Indian Institute of Technology, 721302, Kharagpur, India
2
Theory Division, Saha Institute of Nuclear Physics, 1/AF, BidhanNagar, 700064, Kolkata, India
3
Department of Physics and Meteorology, Indian Institute of Technology, 721302, Kharagpur, India
* e-mail: somdeb.chakraborty@saha.ac.in
Received:
1
March
2011
Accepted:
29
June
2011
Published online:
15
July
2011
We formulate a systematic elegant perturbative scheme for determining the eigenvalues of the Helmholtz equation (∇2 + k
2)
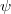= 0 in two dimensions when the normal derivative of 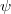vanishes on an irregular closed curve. The unique feature of this method, unlike other perturbation schemes, is that it does not require a separate formalism to treat degeneracies. Degenerate states are handled equally elegantly as the non-degenerate ones. A real parameter, extracted from the parameters defining the irregular boundary, serves as a perturbation parameter in this scheme as opposed to earlier schemes where the perturbation parameter is an artificial one. The efficacy of the proposed scheme is gauged by calculating the eigenvalues for elliptical and supercircular boundaries and comparing with the results obtained numerically. We also present a simple and interesting semi-empirical formula, determining the eigenspectrum of the 2D Helmholtz equation with the Dirichlet or the Neumann condition for a supercircular boundary. A comparison of the eigenspectrum for several low-lying modes obtained by employing the formula with the corresponding numerical estimates shows good agreement for a wide range of the supercircular exponent.
© Società Italiana di Fisica and Springer, 2011
