https://doi.org/10.1140/epjp/s13360-025-06275-3
Regular Article
The dynamical characteristics of interaction solutions for the KP equation describing Rossby waves
1
School of Mathematical Science, Inner Mongolia University, 010021, Hohhot, China
2
College of Science, Inner Mongolia Agriculture University, 010018, Hohhot, China
a
yinxiaojun_2002@163.com
b
smslqs@imu.edu.cn
Received:
17
January
2025
Accepted:
28
March
2025
Published online:
2
May
2025
The extreme weather caused by Rossby waves has been receiving increasing attention due to the presence of the Coriolis force. In this paper, we start with the material conservation equation, utilize the coordinate transformation and the perturbation expansion method to derive the high-dimensional Kadomtsev–Peviashvili equation. N-soliton solutions and K-lump solutions are obtained via the bilinear method and the long-wave limit method. Then, we construct the appropriate auxiliary function to study interaction solutions formed by the above two solutions. By choosing suitable parameters, we gain a clear understanding of the movement trajectories of N-soliton solutions, K-lump solutions, and interaction solutions formed of the above two solutions in different times. It is also evident that the shapes of the solutions do not change during the movement, but when they collide with each other, the amplitude of the solutions will increase significantly. And with the change of time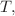 
the relative positions of N-soliton solutions and K-lump solutions will also change.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
