https://doi.org/10.1140/epjp/s13360-025-06172-9
Regular Article
Relation of curvature and torsion of weighted graph states with graph properties and its studies on a quantum computer
Department for Theoretical Physics, Ivan Franko National University of Lviv, 12, Drahomanov St., 79005, Lviv, Ukraine
a
khrystyna.gnatenko@gmail.com
Received:
19
November
2024
Accepted:
24
February
2025
Published online:
19
March
2025
Quantum states of spin systems that can be represented with weighted graphs G(V, E) are studied. The velocity, curvature, and torsion of these states are examined. We find that the velocity of quantum evolution is determined by the sum of the weighted degrees of the nodes in the graph, constructed by raising to the second power the weights of graph G(V, E). The curvature depends on the sum of the weighted degrees of nodes in graphs constructed by raising the weights to the second and fourth powers. It also depends on the sum of the products of the weights of edges forming squares in graph G(V, E). The torsion is related to the sum of the weighted degrees of nodes in graphs constructed by raising the weights to the second, third, and fourth powers, as well as the sum of the products of the weights of edges in graph G(V, E) forming triangles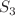 
. Geometric properties of quantum graph states and the sum of the weighted degrees of nodes have been calculated with quantum programming on IBM’s quantum computer for the case of a spin chain.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
