https://doi.org/10.1140/epjp/i2019-12706-y
Regular Article
Generalized Euler, Smoluchowski and Schrödinger equations admitting self-similar solutions with a Tsallis invariant profile
Laboratoire de Physique Théorique, Université de Toulouse, CNRS, UPS, Toulouse, France
* e-mail: chavanis@irsamc.ups-tlse.fr
Received:
17
March
2019
Accepted:
26
April
2019
Published online:
25
July
2019
The damped isothermal Euler equations, the Smoluchowski equation and the damped logarithmic Schrödinger equation with a harmonic potential admit stationary and self-similar solutions with a Gaussian profile. They satisfy an H -theorem for a free energy functional involving the von Weizsäcker functional and the Boltzmann functional. We derive generalized forms of these equations in order to obtain stationary and self-similar solutions with a Tsallis profile. In particular, we introduce a nonlinear Schrödinger equation involving a generalized kinetic term characterized by an index q and a power-law nonlinearity characterized by an index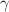 
. We derive an H -theorem satisfied by a generalized free energy functional involving a generalized von Weizsäcker functional (associated with q and a Tsallis functional (associated with 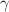. This leads to a notion of generalized quantum mechanics and generalized thermodynamics. When 
, our nonlinear Schrödinger equation admits an exact self-similar solution with a Tsallis invariant profile. Standard quantum mechanics (Schrödinger) and standard thermodynamics (Boltzmann) are recovered for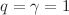 
.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2019
